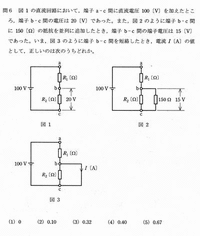
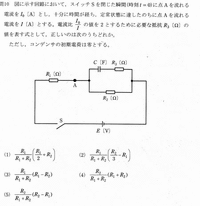
2010年05月24日
■電験3種試験まで【104日】■
CR回路の過渡現象の辺りが理解できました。
キルヒホッフ第2法則で、E=Q/C+IR 式を変形し、I=E/R-Q/CR
C:静電容量(単位:F ファラド)
R:抵抗(単位:Ω オーム)
E:電位差(単位:V ボルト)
I:電流(単位:A アンペア)
Q:電荷量(単位:C クーロン)と時間Tのグラフを描き、Qを時間Tで微分する。
そして、時間T=0の曲線の傾きI=E/R が解かる。
さらに、時間Tが無限大になると、傾きが”0”になる。I=0
よって、Q=CEの漸近線になる。
抵抗器は、両端に電位差が無くなった瞬間に電流を”0”にする。
つまり、電流は非連続性。
しかし、コンデンサは、両端に電位差が無くなった瞬間にも電荷があり、電流を一定時間供給できる。
つまり、電流は連続性。
さらに、続くが…面倒なので、書くのを止めます。では。
キルヒホッフ第2法則で、E=Q/C+IR 式を変形し、I=E/R-Q/CR
C:静電容量(単位:F ファラド)
R:抵抗(単位:Ω オーム)
E:電位差(単位:V ボルト)
I:電流(単位:A アンペア)
Q:電荷量(単位:C クーロン)と時間Tのグラフを描き、Qを時間Tで微分する。
そして、時間T=0の曲線の傾きI=E/R が解かる。
さらに、時間Tが無限大になると、傾きが”0”になる。I=0
よって、Q=CEの漸近線になる。
抵抗器は、両端に電位差が無くなった瞬間に電流を”0”にする。
つまり、電流は非連続性。
しかし、コンデンサは、両端に電位差が無くなった瞬間にも電荷があり、電流を一定時間供給できる。
つまり、電流は連続性。
さらに、続くが…面倒なので、書くのを止めます。では。
Posted by レバレッジ効果 at 20:45 | Comments(0) | 電験3種