■電験３種試験まで【63日】■

■電験３種試験まで【63日】■

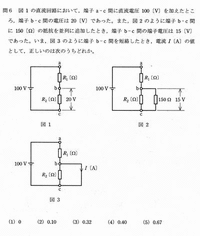
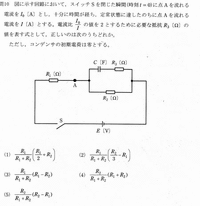
本日は、R-L-C直列や並列回路中の皮相電力、消費電力、無効電力、各電流値を計算する問題にあてました。

電圧の分圧や電流の分流を必ず問われる。

また、電圧や電流はベクトルで考えないと、引っ掛け問題に簡単に引っ掛かります。

ベクトルなので、複素数を用い、表します。

複素数で計算式を表す際、マイナス記号の付け間違いが、まだある。

特に、コンデンサを流れる電流値を計算。

この場合、抵抗値電流から位相が90℃進む（これ基本中の基本！）。

コンデンサのリアクトルの位相90℃遅れと勘違いする。

もっと、複雑な複素数混在式では、注意が必要です。

また、三角関数もベクトル図を描く場合、よく使います。

加法定理や余弦定理など頻繁に使います。

★咲いたコスモス、コスモス咲いた。

sin(a+b)=sin a x cos b + cos a x sin b

★コスコス、シンシン。

cos(a+b)=cos a x cos b － sin a x sin b